Affine Image Registration (follow up, a feature-based approach)

This is a follow up on the previous rigid image registration approach. In the following example I am showing you how to implement an affine transformation registration based on image features with python. In our lab we quite often have to analyze pharmacokinetic parameters based on transient fluorescence imaging taken from tissue in an animal skin flap window. It is the nature of tissues to move during the imaging recording process especially when heat is applied to the tissues. To correct the movement between the individual images, a affine transformation approach is presented to correct the images. 

In a first step, the gradient images are derived from the original images and "landmark" features are detected via threshold criteria (Figure 1).

Figure 1

In a second step, affine transformation is applied to the matching image via optimization method until a defined distance criteria (nearest neighbor criteria with KDTree) between the landmarks reached a minimum (Figure 2).

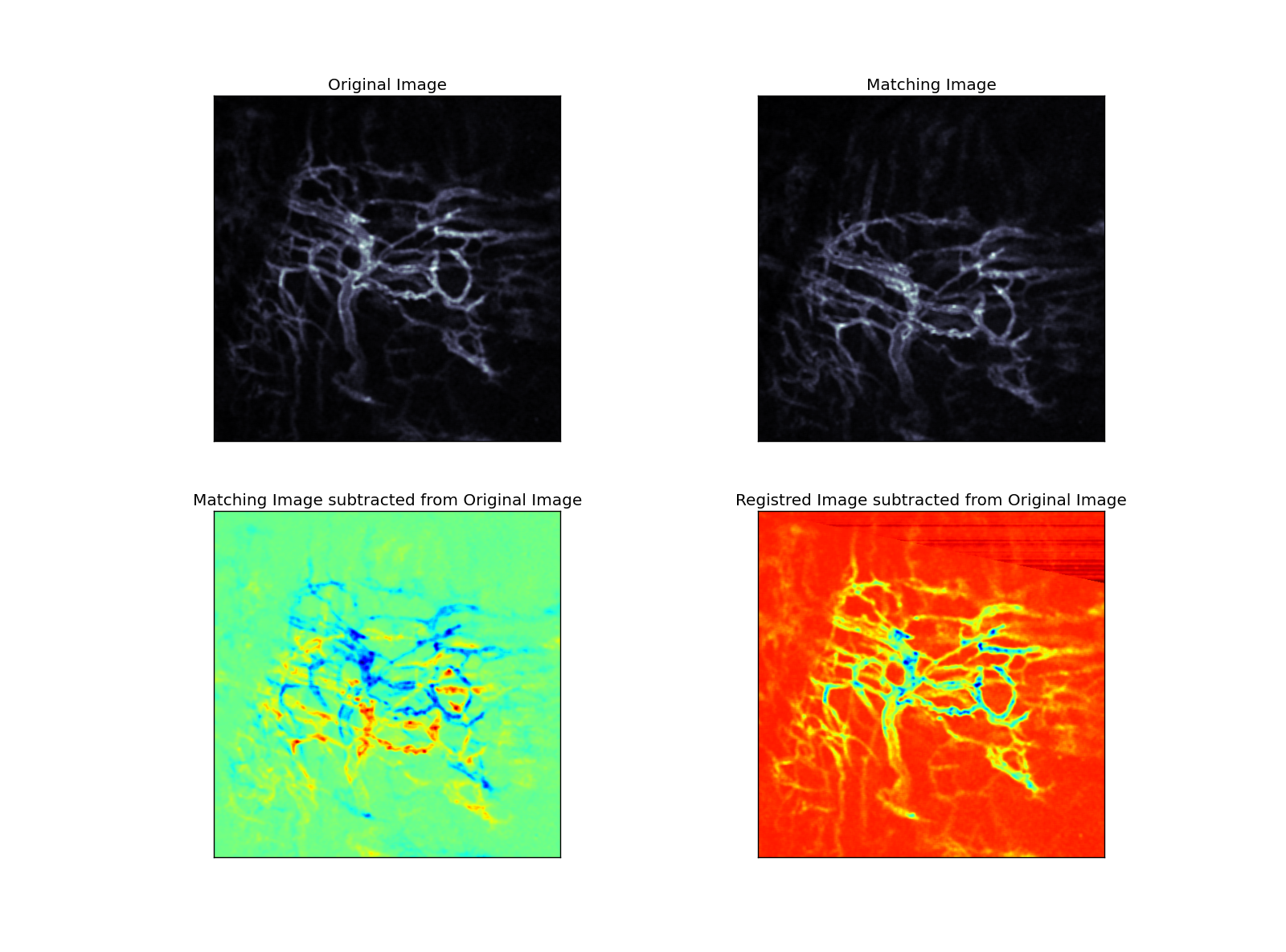Figure 2

The Python code:

       
'''
@author: Christian Rossmann, PhD
@license:  Public Domain
@blog: http://scientificcomputingco.blogspot.com/
'''

from scipy import ndimage
from scipy.spatial import cKDTree
from scipy.optimize import fmin

def register(im1,im2):
    
    # initialize the transformation matrix
    T = [[1.0,0.0],[0.0,1.0]]
    
    # extract features from first image  
    edges1 = ndimage.sobel(im1)
    features1 = dstack(where(edges1.T > edges1.mean()))[0]
    kd = cKDTree(features1)
    
    def errfunction(T,kd=kd,im2=im2):
        
        # transform the image
        img = ndimage.interpolation.affine_transform(im2,T.reshape(2,2))
        
        # extract features from transformed image 
        edges = ndimage.sobel(img)
        features = dstack(where(edges.T > edges.mean()))[0]
        
        dst,idx = kd.query([features])
        
        # measure the distances between features.
        return sum(dst**2)
        
    T = fmin(errfunction,T,xtol=1.e-6,ftol=1.e-6,maxfun=5000,maxiter=5000)
    
    return (T,ndimage.interpolation.affine_transform(im2,T.reshape(2,2)))

im1 = imread("sample_images/IMG1.png")[:,:,0]
im2 = imread("sample_images/IMG2.png")[:,:,0]

im1 = ndimage.filters.uniform_filter(im1,5)
im2 = ndimage.filters.uniform_filter(im2,5)

im1 -= im1.min(); im1 /= im1.max() 
im2 -= im2.min(); im2 /= im2.max()

(T,rimg) = register(im1,im2)

#%%
figure(1)
clf()
s = subplot(1,1,1)
title('Gradient Image with Detected Features')
imshow(edges,'bone')
edges = ndimage.sobel(im1)
features = dstack(where( (edges.T > 0.45) & (edges.T < 0.55) ))[0]
plot(features[:,0],features[:,1],'+',color='red')
xlim([0,im1.shape[0]])
ylim([0,im1.shape[1]])
s.axes.get_xaxis().set_visible(False)
s.axes.get_yaxis().set_visible(False)
#%%
figure(2)
clf()

s = subplot(2,2,1)
title('Original Image')
imshow(im1,'bone')
s.axes.get_xaxis().set_visible(False)
s.axes.get_yaxis().set_visible(False)

s = subplot(2,2,2)
title('Matching Image')
imshow(im2,'bone')
s.axes.get_xaxis().set_visible(False)
s.axes.get_yaxis().set_visible(False)

s = subplot(2,2,3)
title('Matching Image subtracted from Original Image')
imshow(im2-im1,'jet')
s.axes.get_xaxis().set_visible(False)
s.axes.get_yaxis().set_visible(False)

s = subplot(2,2,4)
title('Registred Image subtracted from Original Image')
imshow(rimg-im1,'jet')
s.axes.get_xaxis().set_visible(False)
s.axes.get_yaxis().set_visible(False)

show()

Rigid Image Registration (a quick & dirty intensity-based approach)

Fig. 1. Showing the original image, the manual transformed, and the automatically corrected image via registration algorithm.

Image registration is useful when you want to compare different images from the same object but taken from different angles. In order to make the images comparable, one has to correct the transformation of the target images, so that the target images align with the reference image. This is a quite useful technique with a broad range of applications. One of them is in Medical Imaging where images of the same anatomical structures are taken with different modalities and at different time points.
In this example I am loading good old Lena into the application to demonstrate the function of the code. The important part of this implementation it the finding of initial values (guess) for the fmin (optimization-) function. Without that step, the function is very likely not able to find the correct transformation parameters. Thus, to provide an initial guess, I let the x,y (image shift) and the r (image rotation) vary from -10 to 10 and calculate the intensity-based image errors. Subsequently, the minima for these variations are determined and used as initial guess. (Maybe not the best method but quite simple and robust). Then, I pretty much let the fmin function do the magic to search for the parameters that yield the smallest value returned form the intensity-based image error function.    

The Python code:

       
'''
@author: Christian Rossmann, PhD
@license:  Public Domain
@blog: http://scientificcomputingco.blogspot.com/
'''

import numpy as np
import Image
from scipy import ndimage
from scipy import optimize
from scipy import misc

from pylab import *

def MeasureErr(img1,img2):
    diff = (img1-img2)
    return sum(diff**2)

def RigidRegistration(img,ximg):
    
    # Perform initial guess rotation & translation 
    v_range =  np.array(xrange(-10,10))
    
    err = np.array([MeasureErr(img,ndimage.shift(ximg,(v,0))) for v in v_range])
    x = v_range[where(err==err.min())[0]]
    
    err = np.array([MeasureErr(img,ndimage.shift(ximg,(0,v))) for v in v_range])
    y = v_range[where(err==err.min())[0]]

    err = np.array([MeasureErr(img,ndimage.rotate(ximg,v,reshape=0)) for v in v_range])
    r = v_range[where(err==err.min())[0]]

    # List contains displacement in x and y and rotation
    
    param = [x,y,r]
    
    def ErrFunc(param,img=img,ximg=ximg):
        
        # Perform rotational and translational transformation
        
        _img = ximg.copy()
        _img = ndimage.rotate(_img,param[2],reshape=0)
        _img = ndimage.shift(_img,param[:2])
        
        return MeasureErr(img,_img)

    
    param = optimize.fmin(ErrFunc,param)
    
    #Final transformation
    _img = ximg.copy()
    _img = ndimage.rotate(_img,param[2],reshape=0)
    _img = ndimage.shift(_img,param[:2])
    
    return (_img,param)

img = misc.lena().astype('float32')

# Normalize image (0-1)
img -= img.min() 
img /= img.max()

# Generate transformed image
ximg = img.copy()
ximg = ndimage.shift(ximg,(5,-1))
ximg = ndimage.rotate(ximg,-4,reshape=0)

(rimg,param) =  RigidRegistration(img,ximg)

 
figure(1)
clf()
subplot(1,3,1)
title('Original')
imshow(img)
subplot(1,3,2)
title('Transformed')
imshow(ximg)
subplot(1,3,3)
title('Registered')
imshow(rimg)
show()